Matrix Storage¶

The oneMKL BLAS and LAPACK routines for DPC++ use several matrix and vector storage formats. These are the same formats used in traditional Fortran BLAS/LAPACK.

General Matrix

A general matrix A of m rows and n columns with leading dimension lda is represented as a one dimensional array a of size of at least lda * n. Before entry in any BLAS function using a general matrix, the leading m by n part of the array a must contain the matrix A. The elements of each column are contiguous in memory while the elements of each row are at distance lda from the element in the same row and the previous column.

Visually, the matrix

is stored in memory as an array

Triangular Matrix

A triangular matrix A of n rows and n columns with leading dimension lda is represented as a one dimensional array a, of a size of at least lda * n. The elements of each column are contiguous in memory while the elements of each row are at distance lda from the element in the same row and the previous column.

Before entry in any BLAS function using a triangular matrix,

If upper_lower = uplo::upper, the leading n by n upper triangular part of the array a must contain the upper triangular part of the matrix A. The strictly lower triangular part of the array a is not referenced. In other words, the matrix

is stored in memory as the array
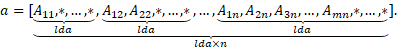
If upper_lower = uplo::lower, the leading n by n lower triangular part of the array a must contain the lower triangular part of the matrix A. The strictly upper triangular part of the array a is not referenced. That is, the matrix

is stored in memory as the array

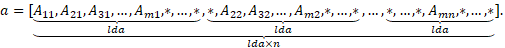
Band Matrix

A general band matrix A of m rows and n columns with kl sub-diagonals, ku super-diagonals, and leading dimension lda is represented as a one dimensional array a of a size of at least lda * n.

Before entry in any BLAS function using a general band matrix, the leading (kl + ku + 1) by n part of the array a must contain the matrix A. This matrix must be supplied column-by-column, with the main diagonal of the matrix in row ku of the array (0-based indexing), the first super-diagonal starting at position 1 in row (ku - 1), the first sub-diagonal starting at position 0 in row (ku + 1), and so on. Elements in the array a that do not correspond to elements in the band matrix (such as the top left ku by ku triangle) are not referenced.

Visually, the matrix A =

is stored in memory as an array

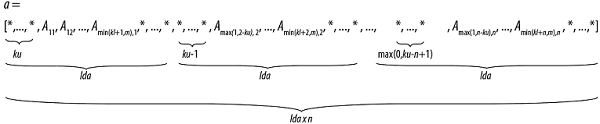The following program segment transfers a band matrix from conventional full matrix storage (variable matrix, with leading dimension ldm) to band storage (variable a, with leading dimension lda):

for (j = 0; j < n; j++) {
    k = ku – j;
    for (i = max(0, j – ku); i < min(m, j + kl + 1); i++) {
        a[(k + i) + j * lda] = matrix[i + j * ldm];
    }
}

Triangular Band Matrix

A triangular band matrix A of n rows and n columns with k sub/super-diagonals and leading dimension lda is represented as a one dimensional array a of size at least lda * n.

Before entry in any BLAS function using a triangular band matrix,

If upper_lower = uplo::upper, the leading (k + 1) by n part of the array a must contain the upper triangular band part of the matrix A. This matrix must be supplied column-by-column with the main diagonal of the matrix in row (k) of the array, the first super-diagonal starting at position 1 in row (k - 1), and so on. Elements in the array a that do not correspond to elements in the triangular band matrix (such as the top left k by k triangle) are not referenced.

Visually, the matrix

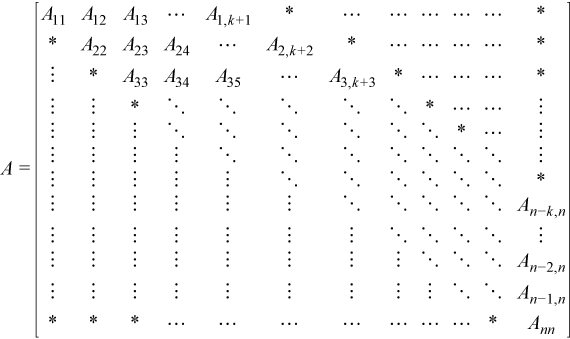
is stored as an array

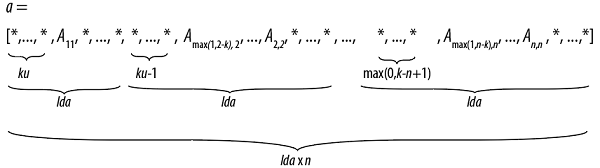
The following program segment transfers a band matrix from conventional full matrix storage (variable matrix, with leading dimension ldm) to band storage (variable a, with leading dimension lda):
```
for (j = 0; j < n; j++) {
    m = k – j;
    for (i = max(0, j – k); i <= j; i++) {
        a[(m + i) + j * lda] = matrix[i + j * ldm];
    }
}
```
If upper_lower = uplo::lower, the leading (k + 1) by n part of the array a must contain the upper triangular band part of the matrix A. This matrix must be supplied column-by-column with the main diagonal of the matrix in row 0 of the array, the first sub-diagonal starting at position 0 in row 1, and so on. Elements in the array a that do not correspond to elements in the triangular band matrix (such as the bottom right k by k triangle) are not referenced.

That is, the matrix

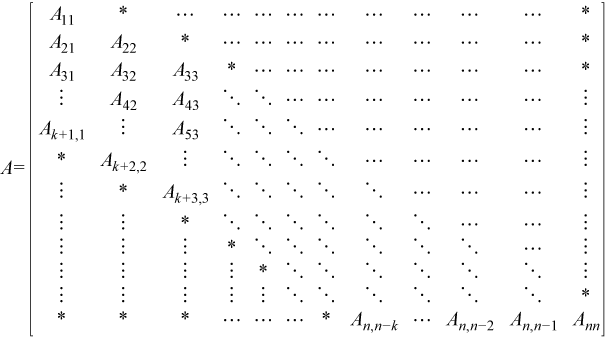
is stored as the array

The following program segment transfers a band matrix from conventional full matrix storage (variable matrix, with leading dimension ldm) to band storage (variable a, with leading dimension lda):
```
for (j = 0; j < n; j++) {
    m = –j;
    for (i = j; i < min(n, j + k + 1); i++) {
        a[(m + i) + j * lda] = matrix[i + j * ldm];
    }
}
```

Packed Triangular Matrix

A triangular matrix A of n rows and n columns is represented in packed format as a one dimensional array a of size at least (n*(n + 1))/2. All elements in the upper or lower part of the matrix A are stored contiguously in the array a.

Before entry in any BLAS function using a triangular packed matrix,

If upper_lower = uplo::upper, the first (n*(n + 1))/2 elements in the array a must contain the upper triangular part of the matrix A packed sequentially, column by column so that a[0] contains A₁₁, a[1] and a[2] contain A₁₂ and A₂₂ respectively, and so on. Hence, the matrix

is stored as the array
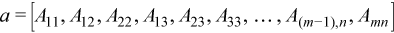
If upper_lower = uplo::lower, the first (n*(n + 1))/2 elements in the array a must contain the lower triangular part of the matrix A packed sequentially, column by column so that a[0] contains A₁₁, a[1] and a[2] contain A₂₁ and A₃₁ respectively, and so on. The matrix

is stored as the array

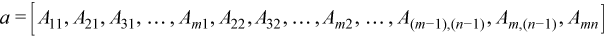
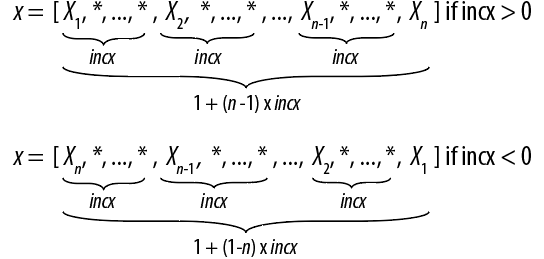
Vector

A vector X of n elements with increment incx is represented as a one dimensional array x of size at least (1 + (n - 1) * abs(incx)).

Visually, the vector

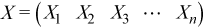
is stored in memory as an array

Parent topic: Dense Linear Algebra