Distributions Template Parameter onemkl::rng::method Values¶
onemkl::rng::method |
Accuracy Flag |
Distributions |
Math Description |
|---|---|---|---|
|
Yes No No No |
|
Standard method. Currently there is only one method for these functions. |
|
No |
|
Generates normally distributed random number x thru the pair of uniformly distributed numbers u1 and u2 according to the formula: |
|
No Yes |
|
Generates normally distributed random numbers x1 and x2 thru the pair of uniformly distributed numbers u1 and u2 according to the formulas: |
|
No Yes Yes No Yes Yes No No No |
|
Inverse cumulative distribution function method. |
|
Yes |
|
For α > 1, a gamma distributed random number is generated as a cube of properly scaled normal random number; for 0.6 ≤α < 1, a gamma distributed random number is generated using rejection from Weibull distribution; for α < 0.6, a gamma distributed random number is obtained using transformation of exponential power distribution; for α = 1, gamma distribution is reduced to exponential distribution. |
|
Yes |
|
For min(p, q) > 1, Cheng method is used; for min(p, q) < 1, Johnk method is used, if q + K·p2+ C≤ 0 (K = 0.852…, C=-0.956…) otherwise, Atkinson switching algorithm is used; for max(p, q) < 1, method of Johnk is used; for min(p, q) < 1, max(p, q)> 1, Atkinson switching algorithm is used (CJA stands for Cheng, Johnk, Atkinson); for p = 1or q = 1, inverse cumulative distribution function method is used;for p = 1 and q = 1, beta distribution is reduced to uniform distribution. |
|
No |
|
(most common): If ν ≥ 17 or ν is odd and 5 ≤ ν ≤ 15, a chi-square distribution is reduced to a Gamma distribution with these parameters: Shape α = ν / 2 Offset a = 0 Scale factor β = 2 The random numbers of the Gamma distribution are generated. |
|
No |
|
Acceptance/rejection method for ntrial·min(p,1 - p)≥ 30 with decomposition into four regions: |
|
No |
|
Acceptance/rejection method for λ≥ 27 with decomposition into four regions: |
|
No No |
|
for λ≥ 1, method based on Poisson inverse CDF approximation by Gaussian inverse CDF; for λ < 1, table lookup method is used. |
|
No |
|
Acceptance/rejection method for large mode of distribution with decomposition into three regions: |
|
No |
|
Acceptance/rejection method for: |
|
No |
|
Multinomial distribution with parameters m, k, and a probability vector p. Random numbers of the multinomial distribution are generated by Poisson Approximation method. |
Note
Accuracy flag represented as a method:
onemkl::rng::<method> | onemkl::rng::accurate
Parent topic: Distributions
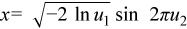
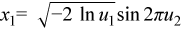
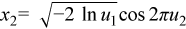
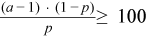 with decomposition into five regions:
with decomposition into five regions: