dot¶

Computes the dot product of two real vectors.

dot supports the following precisions.

T

T_res

float

float

double

double

float

double

Description

The dot routines perform a dot product between two vectors:

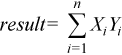
Note

For the mixed precision version (inputs are float while result is double), the dot product is computed with double precision.

dot (Buffer Version)¶

Syntax

void onemkl::blas::dot(sycl::queue &queue, std::int64_t n, sycl::buffer<T, 1> &x, std::int64_t incx, sycl::buffer<T, 1> &y, std::int64_t incy, sycl::buffer<T_res, 1> &result)¶

Input Parameters

queue: The queue where the routine should be executed.
n: Number of elements in vectors x and y.
x: Buffer holding input vector x. The buffer must be of size at least (1 + (n – 1)*abs(incx)). See Matrix and Vector Storage for more details.
incx: Stride of vector x.
y: Buffer holding input vector y. The buffer must be of size at least (1 + (n – 1)*abs(incy)). See Matrix and Vector Storage for more details.
incy: Stride of vector y.

Output Parameters

Syntax

sycl::event onemkl::blas::dot(sycl::queue &queue, std::int64_t n, const T *x, std::int64_t incx, const T *y, std::int64_t incy, T_res *result, const sycl::vector_class<sycl::event> &dependencies = {})¶

Input Parameters

queue: The queue where the routine should be executed.
n: Number of elements in vectors x and y.
x: Pointer to the input vector x. The array holding the vector x must be of size at least (1 + (n – 1)*abs(incx)). See Matrix and Vector Storage for more details.
incx: Stride of vector x.
y: Pointer to the input vector y. The array holding the vector y must be of size at least (1 + (n – 1)*abs(incy)). See Matrix and Vector Storage for more details.
incy: Stride of vector y.
dependencies: List of events to wait for before starting computation, if any. If omitted, defaults to no dependencies.

Output Parameters

Return Values

Output event to wait on to ensure computation is complete.

Parent topic: BLAS Level 1 Routines