dotc¶

Computes the dot product of two complex vectors, conjugating the first vector.

dotc supports the following precisions.

T

std::complex<float>

std::complex<double>

Description

The dotc routines perform a dot product between two complex vectors, conjugating the first of them:

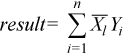
dotc (Buffer Version)¶

Syntax

void onemkl::blas::dotc(sycl::queue &queue, std::int64_t n, sycl::buffer<T, 1> &x, std::int64_t incx, sycl::buffer<T, 1> &y, std::int64_t incy, sycl::buffer<T, 1> &result)¶

Input Parameters

queue: The queue where the routine should be executed.
n: The number of elements in vectors x and y.
x: Buffer holding input vector x. The buffer must be of size at least (1 + (n - 1)*abs(incx)). See Matrix and Vector Storage for more details.
incx: The stride of vector x.
y: Buffer holding input vector y. The buffer must be of size at least (1 + (n - 1)*abs(incy)). See Matrix and Vector Storage for more details..
incy: The stride of vector y.

Output Parameters

Syntax

void onemkl::blas::dotc(sycl::queue &queue, std::int64_t n, const T *x, std::int64_t incx, const T *y, std::int64_t incy, T *result, const sycl::vector_class<sycl::event> &dependencies = {})¶

Input Parameters

queue: The queue where the routine should be executed.
n: The number of elements in vectors x and y.
x: Pointer to input vector x. The array holding the input vector x must be of size at least (1 + (n - 1)*abs(incx)). See Matrix and Vector Storage for more details.
incx: The stride of vector x.
y: Pointer to input vector y. The array holding the input vector y must be of size at least (1 + (n - 1)*abs(incy)). See Matrix and Vector Storage for more details..
incy: The stride of vector y.
dependencies: List of events to wait for before starting computation, if any. If omitted, defaults to no dependencies.

Output Parameters

Return Values

Output event to wait on to ensure computation is complete.

Parent topic: BLAS Level 1 Routines