onemkl::rng::hypergeometric

Generates hypergeometrically distributed random values.

Syntax

template<typename T = std::int32_t, method Method      = h2pe>
  class hypergeometric {
  public:
    hypergeometric(): hypergeometric(1, 1, 1){}
    hypergeometric(std::int32_t l, std::int32_T s,      std::int32_T m)
    hypergeometric(const hypergeometric<T, Method>&      other)
    std::int32_t s() const
    std::int32_t m() const
    std::int32_t l() const
    hypergeometric<T, Method>& operator=(const      laplace<T, Method>& other)
  }

Include Files

• mkl_sycl.hpp

Description

The onemkl::rng::hypergeometric class object is used in the onemkl::rng::generate function to provide hypergeometrically distributed random values with lot size l, size of sampling s, and number of marked elements in the lot m, where l, m, s∈N∪{0}; l≥ max(s, m).

Consider a lot of l elements comprising m “marked” and l-m “unmarked” elements. A trial sampling without replacement of exactly s elements from this lot helps to define the hypergeometric distribution, which is the probability that the group of s elements contains exactly k marked elements.

The probability distribution is given by:)

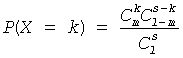
, k∈ {max(0, s + m - l), …, min(s, m)}

The cumulative distribution function is as follows:

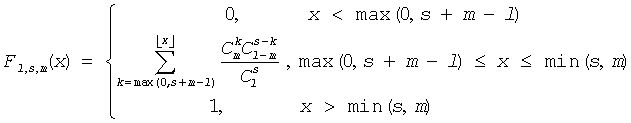
Input Parameters

Name	Type	Description
method	onemkl::rng::method	Generation method. The specific values are as follows: onemkl::rng::h2pe See brief descriptions of the methods in Distributions Template Parameter onemkl::rng::method Values.
l	std::int32_t	Lot size of l.
s	std::int32_t	Size of sampling without replacement .
m	std::int32_t	Number of marked elements m.

Parent topic: Distributions